
Lexer und Parser in Perl zu schreiben, ist keineswegs langbärtigen Gurus vorbehalten. Anhand eines mathematischen Formelparsers erläutert der Snapshot Konzepte und Algorithmen zur Syntaxanalyse und Übersetzung.
Für Compilerbauer und Erfinder neuer Programmiersprachen sind sie das tägliche Brot: Lexer und Parser prüfen beliebig komplexe Ausdrücke auf syntaktische Korrektheit und helfen, sie in Zielsprachen zu übersetzen.
Da Daten heute meist mit XML formatiert sind und einfach zu bedienende XML-Parser zur Verfügung stehen, ist die Kunst des echten Parserschreibens fast in Vergessenheit geraten. Wer allerdings beispielsweise vom Benutzer eingegebene Formeln analysieren und auswerten muss, kommt um einen Parser nicht herum.
 |
| Abbildung 1: Der Lexer zerlegt den Sting in Tokens, der Parser erzeugt den Parse-Tree. Der Übersetzer überführt ihn in die Reverse Polish Notation (RPN) und rechnet mit einem einfachen Algorithmus das Ergebnis aus. |
Um einen Ausdruck wie ``5+4*3'' auszuwerten, muss man ihn zunächst in
Operatoren und Operanden zu zerlegen. Wie Abbildung 1 zeigt,
extrahiert ein sogenannter Lexer zunächst
die Symbole ``5'', ``+'', ``4'', ``*'' und ``3'' aus dem String.
Diese auch Tokens genannten Textstücke werden später an den
Parser gefüttert, der prüft, ob die eingegebene Formel auch
mathematischen Sinn ergibt. Hierzu erzeugt der Parser typischerweise
einen Parse-Baum, der sicherstellt, dass der Ausdruck
einer vorher aufgestellten Grammatik gehorcht. Diese legt Dinge
wie Präzedenz der Operatoren (z.B. Punkt vor Strich) und die Reihenfolge
der Auswertung (Assoziativität, links nach rechts oder umgekehrt)
fest. Steht so die exakte Bedeutung des Ausdrucks fest, kann er
in Programmierschritte übersetzt werden, um ihn mit einem simplen
Verfahren auf dem Computer auszuwerten.
Abbildung 1 zeigt als Beispiel einen
RPN-(Reverse Polish Notation)-Rechner, eine virtuelle
Maschine, die entweder Zahlen oder Operatoren oben auf den Stack wirft und
anschließend versucht, Operand-Operand-Operator-Kombinationen zu
einem Einzelwert reduzieren. So wird aus 4 3 * der Wert 12,
und aus der dann auf dem Stack liegenden Kombination 5 12 + das
Ergebnis der Berechnung: 17.
Zwar könnte man eine String wie ``5+4*3'' einfach an Perls Funktion
eval weitergeben, die ihn dann nach Perls Mathematikregeln auswerten
würde. Doch falls Variablen auftauchen, Operatoren, von denen Perl nichts
weiß, oder gar if-else-Konstrukte erlaubt sind, also letztendlich eine
Mini-Programmiersprache entsteht, dann muss ein
ausgewachsener Parser ran.
Zurück zum Lexer: Auch Leerzeichen sollen im auzuwertenden String
keine Rolle spielen, der Ausdruck ``5 +4 *3'' soll dieselben Symbole liefern
wie ``5+ 4*3''.
Das Lexen ist allerdings nicht immer ganz so
trivial wie im vorgestellten Beispiel. Als Operand könnte
beispielsweise auch eine reelle Zahl wie 1.23E40 auftauchen
oder eine Funktion wie ``sin(x)'', die in die Tokens ``sin('', ``x'' und ``)''
zerlegt werden müsste. Für solche komplexen Lexer gibt es auf dem
CPAN das Modul Parse::Lex. Bei der Installation ist zu beachten, dass
es mindestens Version 0.37 des Moduls Parse::Template benötigt.
Das kurze Skript mathlexer nimmt einen verschachtelten mathematischen
Ausdruck, gibt ihn an den Lexer weiter und lässt diesen die Kombinationen
aus Tokentyp und Tokeninhalt zurückliefern, die anschließend
zu Testzwecken ausgegeben werden.
Das von mathlexer verwendete
Listing MathLexer.pm definiert die Klasse MathLexer, die über
den Konstruktor new einen String zu Analysezwecken entgegennimmt
und gemäß der in der Variablen @tokens abgelegten regulären
Ausdrücke durchforstet. Für jedes gefundene Lexem (die Sequenz der
gefundenen Zeichen, aus denen der Lexer einen Token zusammenstellt), reicht
der mit der Methode next() weitergeschubste Lexer zwei Werte zurück.
Das erste Element des als Referenz zurückgereichten Arrays ist der
Name des gefundenen Tokens (z.B. ``NUM'', ``OPADD'', ``RIGHTP''). Im zweiten
Element folgt dann die tatsächlich gefundene Zeichenkette (z.B. ``4.27e-14'',
``+'', ``)''). Abbildung 2 zeigt die Ausgabe zu Testzwecken, die im wirklichen
Leben als Parserfutter dient.
01 #!/usr/bin/perl -w
02 use strict;
03 use MathLexer;
04
05 my $str = "5*sin(x*-4.27e-14)**4*(e-pi)";
06 print " $str\n\n";
07
08 my $lex = MathLexer->new($str);
09
10 while(1) {
11 my($tok, $val) = $lex->next();
12 last unless defined $tok;
13 printf "%8s %s\n", $tok, $val;
14 }
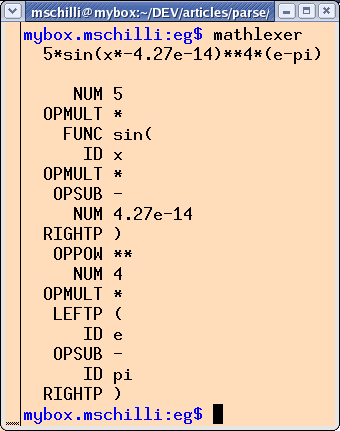 |
| Abbildung 2: Ein von MathParser.pm gelexter mathematischer Ausdruck |
01 ###########################################
02 package MathLexer;
03 ###########################################
04 use strict;
05 use Regexp::Common;
06 use Parse::Lex;
07
08 my @token = (
09 OPPOW => "[*][*]",
10 OPSUB => "[-]",
11 OPADD => "[+]",
12 OPMULT => "[*]",
13 OPDIV => "[/]",
14 FUNC => "[a-zA-Z]\\w*\\(",
15 ID => "[a-zA-Z]\\w*",
16 LEFTP => "\\(",
17 RIGHTP => "\\)",
18 NUM => "$RE{num}{real}",
19 ERROR => ".*", sub {
20 die qq(Can't lex "$_[1]") },
21 );
22
23 ###########################################
24 sub new {
25 ###########################################
26 my($class, $string) = @_;
27
28 my $lexer = Parse::Lex->new(@token);
29 $lexer->skip("[\\s]");
30 $lexer->from($string);
31
32 my $self = {
33 lexer => $lexer,
34 };
35
36 bless $self, $class;
37 }
38
39 ###########################################
40 sub next {
41 ###########################################
42 my($self) = @_;
43
44 my $tok = $self->{lexer}->next();
45 return undef if $self->{lexer}->eoi();
46
47 return $tok->name(), $tok->text();
48 }
49
50 1;
Zu beachten ist, dass Parse::Lex die regulären Ausdrücke als
Strings entgegennimmt. Darum müssen Backslashes als \\ maskiert
werden, wenn ein Symbol wie * nicht als Regex-Metazeichen genutzt wird.
Da Ausdrücke wie \\*\\* schwer zu entziffern sind, verwendet
MathLexer in der ersten Tokendefinition den etwas merkwürdig formulierten
aber identischen Regex "[*][*]".
Ein regulärer Ausdruck, der die vielfältigen Darstellungen von reellen
Zahlen abdeckt (zum Beispiel 1.23E40, .37, 7, 1e10), ist
gar nicht so einfach von Hand zu erstellen. Glücklicherweise bietet
das Modul Regexp::Common vom CPAN bereits vorgekochte Regexen
für allerlei Zwecke, darunter auch einen für reelle Zahlen mit
allerlei Schnickschnack. Nach einem use Regexp::Common im Programm
greift man über einen globalen Hash auf diese Perlen
der Regexkunst zu. Der Ausdruck für reelle Zahlen liegt in
$RE{num}{real}.
Übrigens lässt der Regex $RE{num}{real} auch ein optionales
Minuszeichen vor der reellen Zahl zu. Wegen der gewählten Reihenfolge
der erkannten Lexeme in @tokens wird der Lexer ein vorangestelltes
Minuszeichen aber immer als OP erkennen. Taucht allerdings ein
Minuszeichen im Exponent der reellen Zahl auf, schnappt der Lexer es
als Teil des Lexems NUM auf.
Weiter sorgt Methode skip in Zeile 28 von MathLexer.pm dafür, dass
der Lexer Leerzeichen und Zeilenumbrüche ignoriert. Trifft er allerdings
auf ein Zeichenkonstrukt wie zum Beispiel "}", kommt die in
Zeile 18 definierte ERROR-Pseudo-Token zum Einsatz, das zur Fehlerbehandlung
eine Routine definiert, die einfach mit einem die-Kommando den
Lexer abbricht.
Die syntaktische Gültigkeit eines Ausdrucks untersucht anschließend ein Parser. ``4+*3'' wäre ungültig, der Parser sollte in solchen Fällen einen Fehler melden und das Programm abbrechen. Parser prüfen aber nicht nur die Syntax eines Ausdrucks sondern halten oft auch als Übersetzer her. Während der Parser einen arithmetischen Ausdruck durchkämmt, kann er auch gleich ausrechnen, was dabei herauskommt.
Listing AddMult.yp definiert eine Grammatik für den Parser. Sie
bestimmt, wie der Parser die aus dem Lexer herausströmenden Tokens zu
vorgegebenen Strukturen zusammenfasst. Die erste sogenannte Produktion
expr: add | mult | NUM;
bestimmt, dass der Parser die Sequenz aller Tokens am Ende zu einem Konstrukt
vom Typ expr zusammenfassen muss. Gelingt dies, war der Parser erfolgreich.
Ist dies unmöglich, genügen die Tokens des untersuchten Ausdrucks nicht
der Grammatik. Es liegt ein Syntaxfehler vor und der Parse-Vorgang wird abgebrochen.
01 ###########################################
02 %left OPADD
03 %left OPMULT
04
05 %%
06 expr: add | mult | NUM;
07
08 add: expr OPADD expr {
09 return $_[1] + $_[3]
10 };
11 mult: expr OPMULT expr {
12 return $_[1] * $_[3]
13 };
14 %%
Produktionen wie die oben gezeigte zeigen auf der linken Seite ein sogenanntes
Non-Terminal. Dies ist ein Ausdruck, der sich aus gelexten Tokens
(auch Terminals genannt) zusammensetzt, aber auch weitere Non-
Terminals enthalten kann. expr oben kann zum Beispiel dreierlei
sein, wie die mit ``|'' getrennten Alternativen auf der rechten Seite
des Doppelpunkts zeigen: add (eine Addition), mult (eine
Multiplikation) oder ein Terminal NUM, eine reelle Zahl, die vom
Lexer kommt.
Die Non-Terminals add und mult werden in den nächsten Produktionen
in AddMult.yp definiert. add: expr OPADD expr bestimmt, dass ein
Non-Terminal add sich aus zwei mit dem '+'-Operator verknüpften
expr-Non-Terminals zusammensetzt, die, wie vorher definiert, sich wiederum
aus Additionen, Multiplikationen oder einfachen Zahlen zusammensetzen lassen.
Die Grammatikdatei AddMult.yp dient dem Modul Parse::Yapp als abstrakte
Beschreibung eines Parsers. Sie teilt sich in drei Teile, die jeweils durch
die Zeichensequenz %% voneinander getrennt sind. Oben steht der Header,
der Parserinstruktionen oder Perl-Code beinhalten kann. In der Mitte stehen
die Produktionen der Grammatik und unten schließlich folgt der Footer,
der weiteren Perl-Code definieren kann, in Listing AddMult.yp jedoch
leergelassen wurde. AddMult.yp wird mit der dem Parse::Yapp beiliegenden
Utilty yapp in ein Perl-Modul umgewandelt, das den Parser
implementiert.
Das so entstehende Modul AddMult.pm implementiert einen sogenannten
Bottom-Up-Parser. Dieser liest den Token-Strom aus dem Lexer und
versucht, den in Abbildung 1 gezeigten Parse-Baum von unten nach
oben aufzubauen. Hierzu fasst er gelesene Einheiten gemäß der
Grammatik zu übergeordneten Konstrukten zusammen, solange, bis am Ende
die linke Seite der Startproduktion herauskommt.
Mit jedem Schritt führt der Parser eine von zwei Aktionen aus: Shift oder Reduce. Mit Shift holt der Parser den nächsten Token aus dem Eingabestrom. Mit Reduce fasst der Parser die auf dem Stack liegenden Terminals und Non-Terminals entsprechend der Grammatik zu weiteren Non-Terminals zusammen und 'reduziert' damit die Höhe des Stacks. Ist die Eingabeschlange leer und die letzte Reduktion lässt nur die linke Seite der Start-Produktion auf dem Stack liegen, war der Parse-Vorgang erfolgreich.
Tabelle 1 zeigt, wie ein entsprechend der Grammatik in AddMult.yp
implementierter Bottom-Up-Parser den in Tokens zerlegten Eingabestring
5+4*3 Schritt für Schritt abarbeitet.
Tabelle 1:
+-----+---------------------------+------+---------------+------+
| Step| Rule |Return|Stack |Input |
+-----+---------------------------+------+---------------+------+
| 0 | | | |5+4*3 |
| 1 | SHIFT | |NUM | +4*3 |
| 2 | REDUCE expr: NUM |5 |expr | +4*3 |
| 3 | SHIFT | |expr OPADD | 4*3 |
| 4 | SHIFT | |expr OPADD NUM | *3 |
| 5 | REDUCE expr: NUM |4 |expr OPADD expr| *3 |
| | ***Conflict: Shift/Reduce?| | | |
+-----+---------------------------+------+---------------+------+
In Schritt 0 liegen in der Eingabe die Tokens [NUM, ``5''], [OPADD, ``+''],
[NUM, ``4''], [OPMULT, ``*''] und [NUM, ``3''] vor. In Schritt 1 holt
der Parser die 5 auf den Stack (Shift) und reduziert das NUM-Terminal
in Schritt 2 gemäß der Grammatik (dritte Alternative der ersten Produktion)
zu expr. Anschließend holt der Parser die Tokens
[OPADD, ``+''] und [NUM, ``4''] aus der Eingabe und reduziert letzteren
ebenfalls wieder zu expr. Dann stellt sich die Frage: Was tun?
Der Parser könnte expr OPADD expr gemäß der Grammatik zu expr
reduzieren (zweite Produktion).
Andererseits könnte er auch [OPMULT, ``*''] aus der Eingabe
holen und hoffen, später einmal expr OPMULT expr zu reduzieren
(dritte Produktion).
Grammatiken sind oft nicht eindeutig. Gäbe es beispielsweise nicht
die uralte Mathematikregel ``Punkt vor Strich'', stünde der Parser
bei einem Ausdruck wie ``5+4*3'' vor dem eben erläuterten Shift-Reduce-
Konflikt. Was tun? Im Fall von ``5+4*3'' umschifft die
Präzedenz der Algebra-Operatoren den Konflikt. Der Parser muss
mit dem Reduzieren warten und den Operator * mit shift auf den
Stack hieven, denn * bindet seine Operanden stärker als das
schwache +.
Kommen gleiche Operatoren mehrmals hintereinander zum Einsatz,
wie bei 5-3-2, sind alle Operationen gleichberechtigt und der
Shift-Reduce-Konflikt stellt sich ebenfalls ein. Entscheidet sich
der Parser nach dem Lesen von 5-3 für ein Reduce, wertet
er die Operatoren von links nach rechts aus und verhält sich
damit gemäß den Regeln der Algebra. Ein Shift hätte
den Ausdruck stattdessen wie c<5-(3-2)> ausgewertet, was statt dem
mathematisch erwarteten Wert 0 das überraschende Ergebnis 6
gebracht hätte. Der Minus-Operator nennt man
deswegen links-assoziativ.
Im Fall des Potenzoperators (** in Perl)
erwartet die Algebra übrigens genau
das umgekehrte Verhalten: ``4**3**2'' (``4 hoch 3 hoch 2'') wird
tatsächlich wie 4**(3**2) ausgerechnet. Das lässt sich leicht
in Perl nachprüfen: perl -le 'print 4**3**2' ergibt 262144 (4**9) und
nicht 4096 (64**2).
Diese Mehrdeutigkeit der Grammatik fällt auch dem Parser-Generator
yapp auf, der aus der Datei AddMult.yp das Parser-Modul AddMult.pm
erzeugt:
$ yapp -m AddMult AddMult.yp
4 shift/reduce conflicts
Die ersten zwei Zeilen in Listing AddMult.yp lösen das Problem:
%left OPADD
%left OPMULT
bestimmen, dass sowohl der '+' als auch der '*'-Operator links-assoziativ
arbeiten (also Operationen von links nach rechts vorgenommen werden) und,
wichtiger, dass OPMULT eine höhere Priorität als OPADD besitzt,
da %left OPMULT in einer Zeile nach %left OPADD steht.
Definierte der Parser auch eine OPMINUS Operation mit dem '-'-Operator,
wäre es dringend notwendig, auch %left '-' (und zwar vor der
Definition von OPMULT) einzufügen.
Stünde statt %left '-' im Header der yp-Datei
hingegen %right '-', würde der Parser
Ausdrücke wie 5-3-2 von rechts nach links auswerten. Das
hätte fatale Folgen, denn 5-(3-2) ergibt 6, nicht wie
5-3-2 den Wert 0. Um dem Parser beizubringen, Zahlen zur Potenz zu
erheben, wäre allerdings ein rechts-assoziativer Potenzoperator
%right OPPOW notwendig, und zwar wegen der hohen Priorität der
Potenzoperation nach der Definition on OPMULT.
Mit diesen Tricks läuft der Parser gemäß Tabelle 2 bis zum Ende durch.
Tabelle 2:
+-----+------------------------------+------+---------------------------+------+
| Step| Rule |Return|Stack |Input |
+-----+------------------------------+------+---------------------------+------+
| | ... | | | |
| 6 | SHIFT | |expr OPADD expr OPMULT |3 |
| 7 | SHIFT | |expr OPADD expr OPMULT NUM | |
| 8 | REDUCE expr: NUM | |expr OPADD expr OPMULT expr| |
| 9 | REDUCE expr: expr OPMULT expr|12 |expr OPADD expr | |
| 10 | REDUCE expr: expr OPADD expr |17 |expr | |
+-----+------------------------------+------+---------------------------+------+
Und auch das yapp-Kommando
erzeugt die Datei AddMult.pm jetzt ohne zu meckern. Außer der Grammatik
definiert AddMult.yp neben
manchen Produktionen auch noch ausführbaren Perl-Code.
So legt
mult: expr OPMULT expr {
return $_[1] * $_[3]
};
zum Beispiel fest, dass der Rückgabewert der Produktion (zusätzlich
zum erzeugten Non-Terminal) das Produkt aus den Rückgabewerten der
beiden expr-Ausdrücke ist. So schleift der Parser das Ergebnis des
untersuchten arithmetischen Ausdrucks immer weiter nach oben durch,
bis es schließlich der Startproduktion beiliegt und vom Parser an den
Aufrufer zurückgegeben wird. So wird aus dem Syntaxprüfer automatisch
auch ein Formelberechner. Die Tabellen 1 und 2 zeigen in der
Spalte ``Return'' jeweils den Rückgabewert einer gerade ausgeführten
Reduktion.
Zu beachten ist, dass $_[1] sich in den Codestücken auf den
ersten Ausdruck auf der rechten Seite der Produktion bezieht (also
expr). Die sonst übliche Zählung von 0 gilt hier per Definition
nicht, da $_[0] in Parse::Yapp-Produktionen grundsätzlich eine
Referenz auf den Parser enthält. Enthält eine Produktion mehrere durch
| getrennte Alternativen, kann jede Alternative einen eigenen
Codeblock definieren. Zu beachten ist, dass sich ein Codeblock immer
nur auf die Alternative bezieht, neben der er steht.
Bevor die Parser
zum Einsatz kommt, noch ein Zwischenschritt:
Da das Interface zu yapp-Parsern
etwas exotisch ist und unser MathLexer-Lexer zum Einsatz kommen soll,
wird in Listing MathParser.pm eine einfachere Schnittstelle definiert.
Die Methode parse() von MathParser nimmt so einfach den zu parsenden String
entgegen und liefert das arithmetische Ergebnis zurück.
Im Falle eines Fehlers springt der Parser die in Zeile 28 in MathParser.pm definierte
Routine an und steigt aus.
01 #!/usr/bin/perl
02 use strict;
03 use warnings;
04
05 use MathParser;
06 use AddMult;
07
08 my $mp = MathParser->new(AddMult->new());
09
10 for (qw( 5+2*3 5+2+3 5*2*3 5*2+3)) {
11 print "$_: ", $mp->parse($_), "\n";
12 }
01 ###########################################
02 package MathParser;
03 ###########################################
04 use MathLexer;
05 use strict;
06 use warnings;
07
08 ###########################################
09 sub new {
10 ###########################################
11 my($class, $parser) = @_;
12
13 my $self = {
14 parser => $parser
15 };
16
17 bless $self, $class;
18 }
19
20 ###########################################
21 sub parse {
22 ###########################################
23 my($self, $str, $debug) = @_;
24
25 my $lexer = MathLexer->new($str);
26
27 my $result = $self->{parser}->YYParse(
28 yylex => sub { $lexer->next(); },
29 yyerror => sub { die "Error" },
30 yydebug => $debug ? 0x1F : undef,
31 );
32 }
33
34 1;
Listing mathparser zeigt eine einfache Anwendung, die MathParser.pm nutzt
und vier verschiedene
Ausdrücke parst und auswertet:
5+2*3: 11
5+2+3: 10
5*2*3: 30
5*2+3: 13
Es zeigt sich, dass der Parser die Präzedenzregeln beachtet und
die Ausdrücke korrekt wie 5+(2*3) und (5*2)+3 ausführt.
Der Präzedenzkonflikt lässt sich auch anders lösen: Wird die Grammatik wie in
UnAmb.yp umformuliert, ergibt sich die höhere Präzedenz des '*'-Operators
einfach aus den Zusammenhängen zwischen den Produktionen. Eine Multiplikation
wird zunächst in dem Non-Terminal term zusammengefasst, bevor
eventuell bestehende Additions-Reduktionen ausgeführt werden.
01 %%
02 expr: expr OPADD term {
03 return $_[1] + $_[3];
04 }
05 | term {
06 return $_[1];
07 };
08
09 term: term OPMULT NUM {
10 return $_[1] * $_[3];
11 }
12 | NUM {
13 return $_[1];
14 };
15 %%
Mit
diesem Verfahren lässt sich auch das Verhalten von im Eingabestring
zugelassenen Klammern implementieren, um zum Beispiel ``(5+4)*3'' zu
erzwingen. Hierzu wird einfach die term-Produktion umdefiniert
und eine weitere Produktion force hinzugefügt:
term: term OPMULT force
{ ... }
| force
force: LEFTP expr RIGHTP
{ return $_[2]; }
| NUM
Nun genießen geklammerte Ausdrücke höchste Priorität und werden noch vor den Multiplikationen ausgeführt.
Statt den arithmetischen Ausdruck direkt auszuwerten, bietet es sich an,
ihn in eine leicht berechenbare Form wie RPN zu überführen. Listing
RPN.yp zeigt die zugehörige Grammatik. Nur die Codestücke
an den Produktionen wurden verändert. Sie geben nun nicht mehr
berechnete Werte weiter, sondern schieben Zahlen und Operationen nach
RPN-manier in einen Array, der als Referenz Stufe um Stufe zurückgereicht wird
und schließlich beim Aufrufer des Parsers ankommt.
01 %left OPADD
02 %left OPMULT
03
04 %%
05 expr: add
06 | mult
07 | NUM { return [ $_[1] ]; };
08
09 add: expr OPADD expr {
10 return [
11 @{$_[1]}, @{$_[3]}, $_[2]
12 ];
13 };
14
15 mult: expr OPMULT expr {
16 return [
17 @{$_[1]}, @{$_[3]}, $_[2]
18 ];
19 };
20 %%
01 #!/usr/bin/perl
02 use strict;
03 use warnings;
04
05 use MathParser;
06 use RPN;
07
08 my $mp = MathParser->new(RPN->new());
09
10 for my $string (qw(5+4+3 5+4*3)) {
11 print "$string: [";
12 for (@{ $mp->parse($string) }) {
13 print "$_, ";
14 }
15 print "]\n";
16 }
rpn ist das zugehörige aufrufende Skript und
erzeugt -- wie erwartet -- grundsätzlich unterschiedliche Umwandlungen
für 5+4*3 und 5+4+3:
5+4+3: [5, 4, +, 3, +, ]
5+4*3: [5, 4, 3, *, +, ]
Im oberen Ausdruck geht der Übersetzer einfach stur von links nach rechts durch und addiert die Einzelwerte nacheinander auf. Zuerst werden 5 und 4 addiert, dann zum Ergebnis 3 hinzugezählt.
Im unteren Ausdruck dürfen 5+4 jedoch
wegen der ``Punkt-vor-Strich''-Regelung nicht sofort addiert werden.
Vielmehr schiebt der Übersetzer
zunächst die nächste Zahl 3 auf den Stack, führt die dann verlangte
Multiplikation aus und addiert das Ergebnis erst danch zur weiter
unten im Stack stehenden 5.
Zum Thema Parsen gibt es reichlich Bücher, das Drachenbuch [2] ist
der Klassiker unter ihnen. Es ist nicht ganz einfach zu lesen, aber unverzichtbar.
Neben dem besprochenen Bottom-Up-Parser-Generator Parse::Yapp, der
an die Unix-Tools lex und yacc ([5]) angelehnt ist,
führt das CPAN auch noch
den Top-Down-Parser-Generator Parse::RecDescent,
der dank der unterschiedlichen Parse-Technologie völlig der andere Charakteristiken
aufweist und in [4] (ebenso wie Parse::Yapp)
angerissen wird. Und letztlich kann man Parser auch von
Hand schreiben. Besonders mit funktionaler Programmierung geht das sehr
effektiv, wie [3] und [6] beschreiben.
 |
Michael Schilliarbeitet als Software-Engineer bei Yahoo! in Sunnyvale, Kalifornien. Er hat "Goto Perl 5" (deutsch) und "Perl Power" (englisch) für Addison-Wesley geschrieben und ist unter mschilli@perlmeister.com zu erreichen. Seine Homepage: http://perlmeister.com. |