Anhand von Trainingsdaten in Form von täglich im Auto erfassten Kilometerständen versucht ein KI-Programm, Muster im Fahrverhalten zu erlernen und Prognosen für die Zukunft abzugeben.
In der Rubrik "Deep Learning" sprudeln die Neuerscheinugen zur Zeit ja nur so aus den Verlagen heraus, "Neuronale Netzwerke" hier, "Entscheidungsbäume" da, und mit brandaktuellen Open-Source-Tools wie "Tensorflow" oder "Scikit" kann selbst Otto Normalverbraucher seinem Heim-PC künstliche Intelligenz einhauchen. Was läge näher, als den lerneifrigen Rechner mit gesammelten Daten zu füttern, und zu prüfen, ob er dann anhand historischer Werte und mittels KI-Techniken die Zukunft vorhersagen kann?
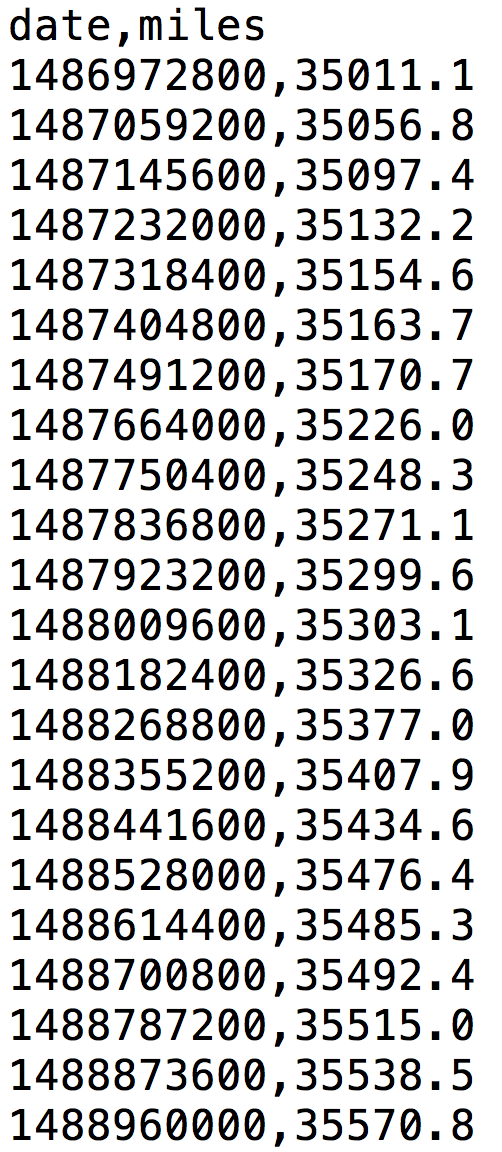
Wie in einer früheren Ausgabe dieser Reihe schon einmal besprochen, habe ich einen Adapter im Auto stecken, der über den OBDII-Port Fahrdaten sammelt und sie übers Handy-Netzwerk auf einem Webservice hinterlegt ([2]). Diese Daten holen dann Skripts per REST-API vom Netz und können damit minutiös belegen, wer wann mit dem Auto wohin gefahren ist. So ist es zum Beispiel ein Leichtes, tägliche Kilometerstände abzurufen und als CSV-Datei auszugeben (Abbildung 1) oder, wie in Abbildung 2 gezeigt, die Tachodaten eines Jahres grafisch über die Zeitachse aufzutragen.
| |
| Abbildung 1: CSV-Datei mit täglichem Kilometerstand des Autos. |
 |
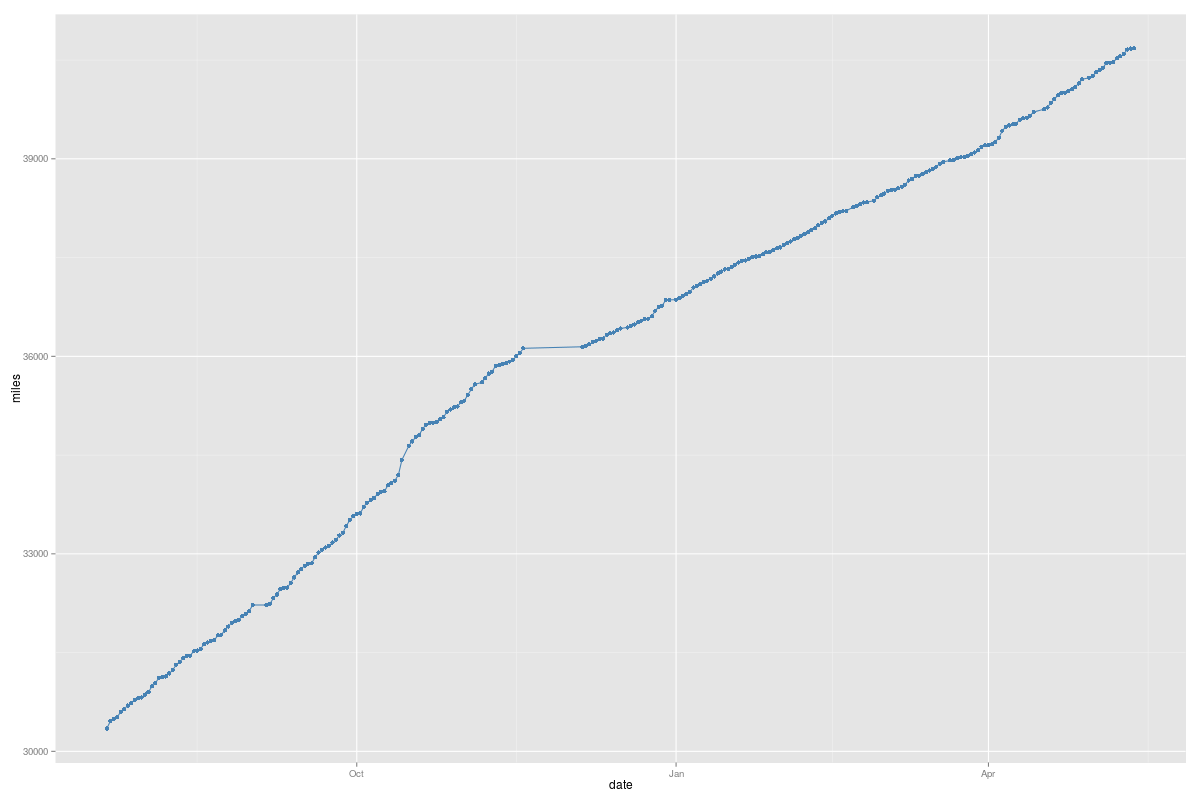| Abbildung 2: Regelmäßig abgelesene Tachostände über ein Jahr aufgetragen. |
Der abgesehen von ein paar Rucklern lineare Verlauf der Kilometerstände deutet darauf hin, dass das Auto fast jeden Tag eine stattliche Anzahl von Kilometern abspult, und falls jemand fragte: "Was wird der Tacho nächstes Jahr im Juli anzeigen?", könnte ein mathematisch geschulter Mensch mittels Dreisatz relativ zügig den zukünftigen Kilometerstand errechnen. Doch wie steht's mit den heute verfügbaren KI-Programmen, wie aufwändig wäre es, die historischen Daten einzufüttern, den Computer den Tachoverlauf lernen zu lassen, damit er später akkurate Zukunftsprognosen erstellen kann?
Heute erhältliche KI-Tools sind von Hexenwerk noch weit entfernt und erfordern schon noch, dass man die Rahmenbedingungen genau absteckt, bevor der Computer überhaupt etwas erkennt. Ist der lineare Verlauf der Kurve bekannt, wählt der Fachmann ein KI-Tool für lineare Regression, dann ist der Erfolg vorprogrammiert.
Tensorflow, eines der ganz heißen KI-Frameworks aus dem Hause Google, hilft auf
hoher Abstraktionsebene beim Einfüttern von Daten, sowie beim Trainieren und
Auswerten von Modellen. Und da KI-Tools relativ viel mit linearer Algebra und
Matrizen rechnen, helfen auch Mathe-Tools wie Pythons "Pandas" bei der Arbeit.
Tensorflow für python3 installiert sich auf Ubuntu einfach mit dem
Python-Modul-Installer pip3 install tensorflow, gleiches gilt für Pandas und
andere Module. Bei meiner Installation warf der Tensorflow-Engine bei
jedem Aufruf mit wüsten Warnungen um sich, die sich durch
Setzen der Environment-Variable TF_CPP_MIN_LOG_LEVEL auf den Wert 3
jedoch abstellen ließen.
Tensorflow erwartet die mathematischen Gleichungen zum Betreiben eines
Modells als sogenannte "Nodes" in einem Graphen, den es in "Sessions"
mit Parametern füllt und wieder und wieder ausführt, entweder auf einem
einzigen PC oder auch gerne parallel auf ganzen Clustern von Maschinen
im Rechenzentrum. Listing 1 definiert die Geradengleichung für das
lineare Modell in Zeile 23 als Y=X*W+b.
Die Variable X ist hier der Eingabewert für die Simulation,
gibt also den Zeitwert vor, zu dem das Verfahren den Kilometerstand Y
als Ausgabe errechnet. Die Parameter W ("weight") und b ("bias")
zum Multiplizieren von X beziehungsweise zum Addieren eines Offsets
soll das Modell im Training bestimmen, und zwar so, dass Y möglichst
genau dem Kilometerstand im Training zum Zeitpunkt X entspricht.
01 #!/usr/bin/env python3
02 import pandas as pd
03 import tensorflow as tf
04 import numpy
05 import os
06
07 os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
08
09 rnd = numpy.random
10 learning_rate = .01
11 training_epochs = 2000
12 chkpoint = 250
13
14 train_df = pd.read_csv("odometer.csv")
15
16 X = tf.placeholder("float")
17 Y = tf.placeholder("float")
18
19 W = tf.Variable(rnd.randn(), name="weight")
20 b = tf.Variable(rnd.randn(), name="bias")
21
22 # model: Y = X*W + b
23 pred = tf.add(tf.multiply(X, W), b)
24
25 # mean squared error
26 total = len(train_df.index)
27 cost = tf.reduce_sum(
28 tf.pow(pred-Y, 2))/(2*total)
29
30 # normalize training set
31 nn_offset=int(train_df[['date']].min())
32 nn_div=int(train_df[['date']].max() -
33 train_df[['date']].min())
34 print("norm_off=", nn_offset)
35 print("norm_mult=", nn_div)
36 train_df['date'] -= nn_offset
37 train_df['date'] /= nn_div
38
39 opt = tf.train.GradientDescentOptimizer(
40 learning_rate).minimize(cost)
41
42 init = tf.global_variables_initializer()
43
44 # tensorflow session
45 with tf.Session() as sess:
46 sess.run(init)
47 for epoch in range(training_epochs):
48 for ix, row in train_df.iterrows():
49 sess.run(opt, feed_dict={
50 X: row['date'],
51 Y: row['miles']})
52 if epoch % chkpoint == 0:
53 c=sess.run(cost, feed_dict={
54 X: train_df['date'],
55 Y: train_df['miles']})
56 print("W=", sess.run(W),
57 "b=", sess.run(b),
58 "cost=", c)
Hierzu definieren die Zeilen 16-17 die Variablen X und Y als
"placeholder", und die Zeilen 19-20 die Parameter W und b als
"Variable" und initialisieren sie mit zufälligen Werten aus der
Random-Bibliothek des numpy-Moduls.
Zeile 14 liest in einem Rutsch die in zwei Spalten date und miles
vorliegenden Daten der CSV-Datei in einen Pandas-Dataframe ein, einer
Art Tabelle mit zwei Spalten.
Das eigentliche Training übernimmt der Optimizer in Zeile 39, der nach dem
Gradient-Descent-Verfahren versucht, die Geradengleichung durch Modifizieren
der Parameter W und b solange an die Einzelpunkte aus den Trainingsdaten
anzupassen, bis die in Zeile 27 definierte Kosten- (oder Fehler-) Kalkulation
cost auf einen minimalen Wert fällt. Sie definiert dazu, auch wieder in
Tensorflow-Semantik, die mittlere quadratische Abweichung aller Trainingspunkte
von der durch W und b bestimmten Geraden.
In der ab Zeile 45 laufenden Tensorflow-Session iteriert die For-Schleife
ab Zeile 47 über alle in Zeile 11 festgesetzten 2000 Trainingseinheiten
und berechnet alle 250 Durchgänge den Wert für die Kostenfunktion, um den
User bei Laune zu halten. Fürs Training muss Tensorflow aber letztlich
nur in Zeile 49 mit run die Session mit den aktuellen X- und Y-Werten
aufrufen, die dann über den Optimizer im Hintergrund die Formel in Zeile 23
aufruft, das Ergebnis ausrechnet und ihrerseits über die Kostenfunktion
die Parameter weiter anpasst.
Nach 2000 Durchgängen zeigt sich das Bild in Abbildung 3, der Wert
für B pendelt sich auf 6491 ein, der für b auf 32838.
 |
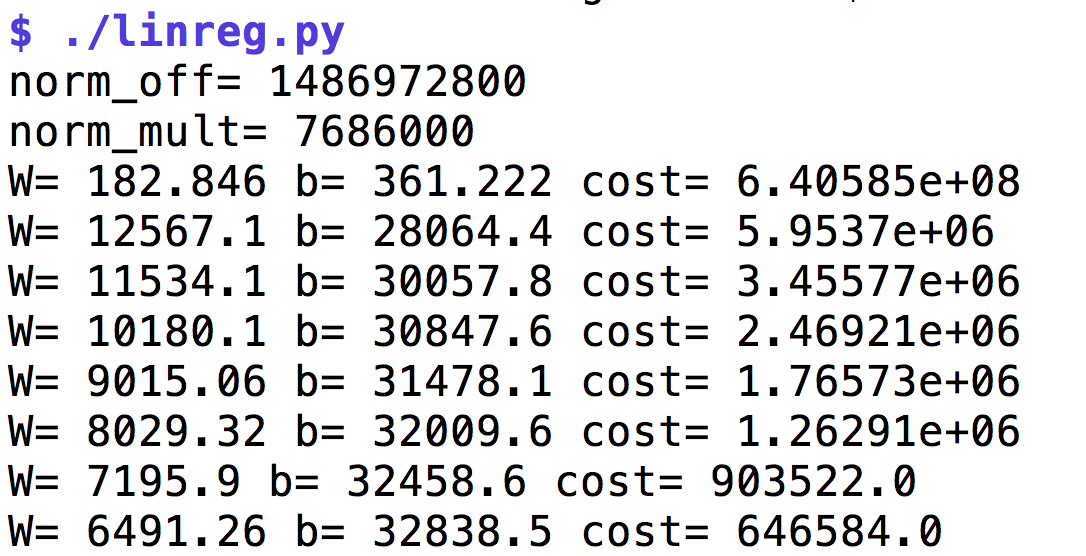| Abbildung 3: Der Lern-Algorithmus minimiert schrittweise die als Kosten bezeichneten Abweichungen. |
Allerdings klappt die Regression nur, falls die Trainingsdaten vorher auf einen
begrenzten Wertebereich normalisiert wurden. Füttert das Skript etwa den
Optimizer mit den unmodifizierten Unix-Sekunden, schaukelt sich der auf
und produziert immer unsinnigere Werte, bis er schließlich die Grenzen der
Fließkommazahlen sprengt und alle Parameter auf nan ("not a number") setzt.
Deshalb normalisieren die Zeilen 31-37 die Trainingsdaten vorab nach der
Min-Max-Methode, finden mit den Pandas-Methoden min() und max() den
minimalen und den maximalen Zeitstempelwert, ziehen ersteren als Offset von
allen Trainingswerten ab und dividieren sie anschließend durch die
Min-Max-Differenz. Heraus kommen normalerweise Trainingswerte zwischen
0 und 1 (aber Achtung falls min=max!), die der Optimizer besser verarbeitet.
Mit den gelernten Parametern lassen sich nun im Rahmen des Modells
historische Werte reproduzieren oder auch die Zukunft voraussagen.
Welchen Kilometerstand wird das Auto am 2. Juni 2019 aufweisen? Das
Datum hat einen Epoch-Wert von 1559516400, den das Modell genau wie
im Trainingsfall erst normalisieren muss. Der in Abbildung 3 gefundene
Offset norm_off von 1486972800 wird abgezogen und das Eingabedatum
auch noch durch den Skalierungsfaktor
norm_mult von 7686000 geteilt. Es ergibt sich ein X-Wert von 9.43, der in
die Formel Y=X*W+b eingesetzt einen Kilometerstand von 94.115 voraussagt.
Alles unter der Annahme natürlich, dass das Modell stimmt, also ein
linearer Anstieg vorliegt, und dass die drei Monate Trainingsdaten
für die genaue Ermittlung des Anstiegs ausreichten.
Um sicher zu stellen, dass das Modell nicht nur die Trainingsdaten simuliert, sondern auch die Wirklichkeit vorhersagt, teilen KI-Fachkräfte die vorliegenden Daten oft in ein Training- und ein Testset auf. Trainiert wird das Modell nur mit Daten aus ersterem, denn sonst besteht die Gefahr, dass es zwar minutiös die Trainingsdaten nachahmt, aber auch temporäre Ausreißer nachbildet, die in der Produktion dann später nicht mehr vorkommen, und Artefakte vorhersagt, die dann nicht eintreffen. Bleibt das Testset bis zum Abschluss des Trainings unangetastet, und sagt danach das Modell auch die Testdaten richtig voraus, wird sich das KI-System aller Wahrscheinlichkeit nach auch später in der Produktion richtig verhalten.
Nun konnte mein HP-41CV Taschenrechner vor 30 Jahren aus einer Ansammlung von x/y-Werten und der Annahme eines linearen Zusammenhangs auch schon mittels linearer Regression die Parameter W und b bestimmen. Allerdings kann Tensorflow nun weit mehr, denn neben komplexeren Regressionstechniken versteht es auch neuronale Netzwerke und Decision Trees.
Wer mit Adleraugen auf die Kilometerstände schaut, stellt fest, dass der Zuwachs keineswegs genau linear mit der Zeit erfolgt. Abbildung 4 zeigt den höher aufgelösten Kilometerzuwachs pro Tag, und es ist offensichtlich, dass der Anstieg gewaltigen Schwankungen unterliegt. So bewegt sich das Auto an den meisten Tagen zwischen 30 und 90 Kilometern, während es hin und wieder ein oder zwei Tage lang kaum fährt und oft ganz still steht.
 |
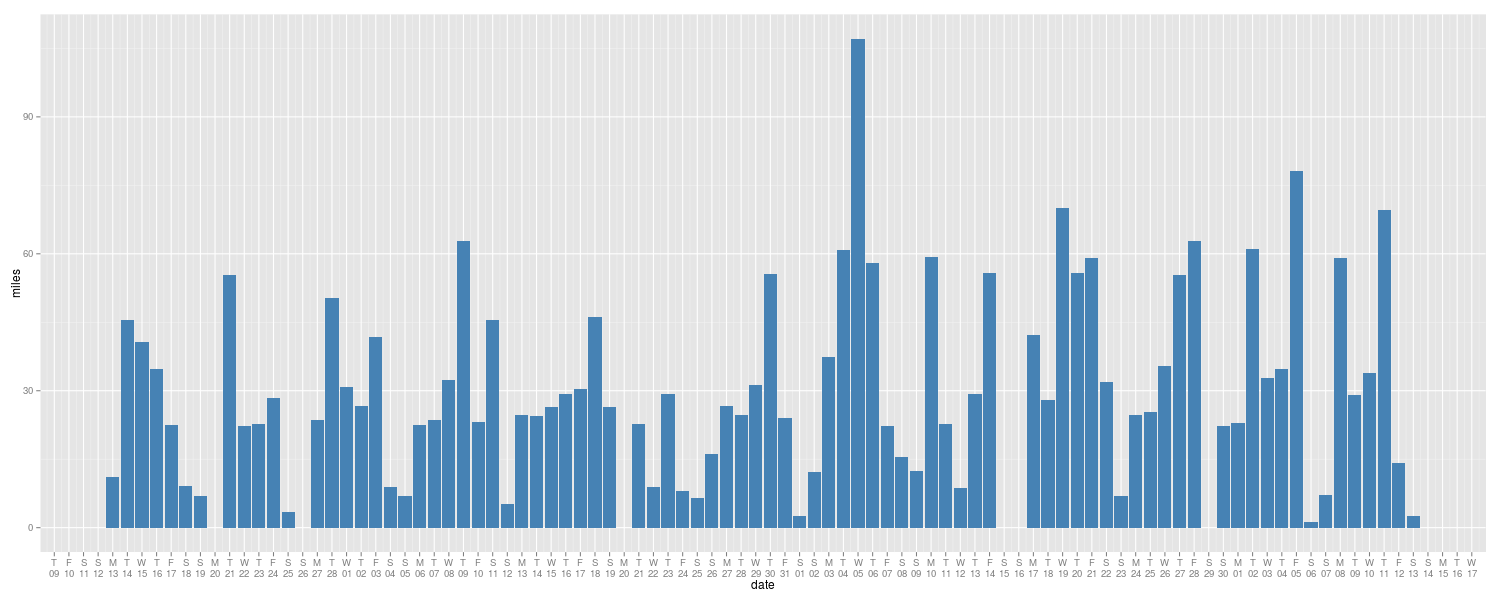| Abbildung 4: Pro Tag gefahrene Strecke über die letzten drei Monate. |
Ein Mensch schaut sich einfach den Graphen in Abbildung 2 an, und zack! ist klar, dass der Wagen am Wochenende weniger als an Werktagen herumkesselt. Damit ein KI-System die gleiche Leistung erbringt, muss es der programmierende Mensch erst mal an die Hand nehmen und in die richtige Richtung leiten.
Liegen die Datumsangaben zum Beispiel wie in Unix üblich als Epoch-Sekunden vor, findet das KI-System nie im Leben heraus, dass alle 7 Tage Wochenende mit weniger Fahrbetrieb ist. Eine lineare Regression würde höchstens die letzten paar Datenpunkte in die Zukunft strecken, ein Polynomregression gar im Overfitting-Rausch völlig irre Patterns produzieren.
 |
| Abbildung 5: Wochentag als Krücke für das neuronale Netzwerk |
Lernalgorithmen kommen auch schlecht mit unvollständigen Daten zurecht.
Fehlen Messwerte, wie zum Beispiel an Tagen, an denen das Auto nur
in der Garage stand, füllt der gewissenhafte Maschinenlehrer sie mit
sinnvollen Werten, wie zum Beispiel Nullen auf. Und er fügt das hinzu,
was in der Disziplin Machine Learning als "Expert Knowledge" gilt: Da
der Wochentag der Datumswerte bekannt ist und dem Algorithmus hoffentlich
weiterhilft, stellt eine neue CSV-Datei miles-per-day-wday.csv einfach
die laufende Nummer des Wochentags (Strings mögen neuronale Netzwerke
nicht, nur Zahlen) dem abgelesenen Tageskilometerstand entgegen (Abbildung 5).
01 #!/usr/bin/python3
02 import pandas as pd
03
04 from sklearn.model_selection \
05 import train_test_split
06 from sklearn.preprocessing \
07 import StandardScaler
08 from sklearn.neural_network \
09 import MLPClassifier
10
11 train_df = \
12 pd.read_csv("miles-per-day-wday.csv")
13 X = train_df.drop('weekday', axis=1)
14 y = train_df['weekday']
15
16 X_train, X_test, y_train, y_test = \
17 train_test_split(X, y)
18
19 scaler = StandardScaler()
20 scaler.fit(X_train)
21 X_train_n = scaler.transform(X_train)
22 X_test_n = scaler.transform(X_test)
23
24 mlp = MLPClassifier(
25 hidden_layer_sizes=(1,1,1),max_iter=40000)
26 mlp.fit(X_train_n,y_train)
27
28 #print(mlp.predict(X_test_n))
29
30 single=pd.DataFrame([[1]],columns=['miles'])
31 print(mlp.predict(scaler.transform(single)))
Listing 2 nutzt dann das Framework sklearn zum Aufbau eines neuronalen
Netzwerks, das das mit Kilometerständen trainiert, um den zugehörigen
Wochentag zu erraten. Es liest zunächst die CSV-Datei ein und formt daraus
den Dataframe X mit den Kilometerständen und y als Vektor mit den
zugehörigen Wochentagsnummern. Die Funktion train_test_split() spaltet
die vorliegenden Daten in ein Trainings- und ein Testset auf, die
der Standard-Skalierer in den Zeilen 19-22 normalisiert, denn neuronale
Netzwerke sind extrem pinibel, was den Wertebereich der Eingabewerte
angeht.
Das in Zeile 24 erzeugte Multi-layer-Perceptron vom Typ MLPClassifier spannt
das neuronale Netzwerk mit zwei Layern auf, und schreibt vor, dass das Training
maximal 1000 Schritte dauern darf. Der Aufruf der Methode fit() führt dann
das Training durch, bei dem der Optimierer versucht, im sogenannten "Supervised
Learning" die internen Rezeptorenverstärker zur Bewertung der Eingabe so lange
zu verstellen, bis sich der Fehler zwischen dem aus dem Trainingsparameter
errechneten Vorhersage und dem Erwartungswert in y_train minimiert. Das
Ergebnis war im Versuch nicht berauschend, teilweise variierten die
vorhergesagten Werte stark von Aufruf zu Aufruf und die Präzision ließ zu
wünschen übrig. Eine Reihe verschiedenartiger Eingabeparameter würden zu
besseren Ergebnissen führen.
Insgesamt stehen mit Tensorflow und Scikit zwei ausgereifte Frameworks zum Experimentieren mit KI-Anwendungen zur Verfügung. Der Einstieg ist nicht ganz von Pappe, da die Literatur zu den allerneuesten Errungenschaften noch sehr jung und unausgereift ist, und eine ganze Reihe von Werken sich erst noch im Entwicklungsstadium befindet. Es lohnt sich aber auf jeden Fall, sich in die Materie einzuarbeiten, denn dem Aufgabenfeld steht eine rosige Zukunft bevor.
Listings zu diesem Artikel: http://www.linux-magazin.de/static/listings/magazin/2017/05/snapshot/
Michael Schilli, "Wege zum Connected Car": Linux-Magazin 10/16, S.84, http://www.linux-magazin.de/Ausgaben/2016/10/Perl-Snapshot
"Introduction to Machine Learning with Python", Sarah Guido, Andreas C. Müller, O'Reilly Media, 2016
"Hands-On Machine Learning with Scikit-Learn and Tensorflow", Aurélien Géron, O'Reilly Media, 2017
 |
Michael Schilliarbeitet als Software-Engineer in der San Francisco Bay Area in Kalifornien. In seiner seit 1997 laufenden Kolumne forscht er jeden Monat nach praktischen Anwendungen verschiedener Programmiersprachen. Unter mschilli@perlmeister.com beantwortet er gerne Ihre Fragen. |